これから花形になるであろう最先端のデータサイエンティストやAIエンジニアにとって、これから話すようなことは寝ててもわかるようなことばかりかもしれません。
ここでは、それ以外の普通のITエンジニアが、実践としてAI(人工知能)を使うことを想定し、道しるべになることなどを述べていきたいと思います。
■ AIプログラミング
AI は、Pythonを使った プログラミングによってつくられます。
一般的なITエンジニアにとって、AIプログラミング の3種の神器と言えば、次の3つです。
1)Python
スクリプト言語のため習得が容易
また、ネットワーク機能、データ分析機能などを提供してくれるパッケージが豊富
2)TensorFlow / Keras
ディープラーニング機能が用意に使えるパッケージ
3)Pandas or Numpy
学習データを入れる配列。学習データを編集する機能が充実している
普通のプログラミングと異なるのは、次の2つの工程のプログラミングが必要になる点です。
①学習前の AIを創るためのプログラミング
②学習後の AIを使うためのプログラミング
プログラミングである以上、両方とも、ロジックを組むことに変わりはありません。
特に、②の学習後の AIを使うプログラミングは、通常通り、パラメータを指定して関数を呼び出し、結果を得るだけです。
特殊なのは、①の学習前の AIを創るプログラミングです。「AIプログラミング」とは、この学習前の AI を創ることを意味します。AIプログラミング の目的は、ロジックを組むということではなく、使えるモデルを完成させることが目的となります。
AIプログラミングでは、以下の2つの作業を実施することになります。
①モデルの作成
②モデルの学習と評価
ただ、一回でこのサイクルが終わることはなく、モデルと学習データに変更を加えながら何度も繰り返すことになります。
ロジックとは、条件に従って関数を呼び出すことで想定した処理結果を得られる手順を表現したものですが、
AI プログラミングにおいて、ロジックに相当するものは、AIのモデル(形状)を表現するコードです。
一見、単に、決まった順番で、特定の関数を呼び出しているだけのように見えますが、はたして正しい処理結果を返すモデルなのかは、学習してみないとわかりません。
■ モデルの作成
モデルの実際のコーディング例を以下に示します。
(TensolFlowのチュートリアル(回帰:燃費を予測する)より引用し、改編)
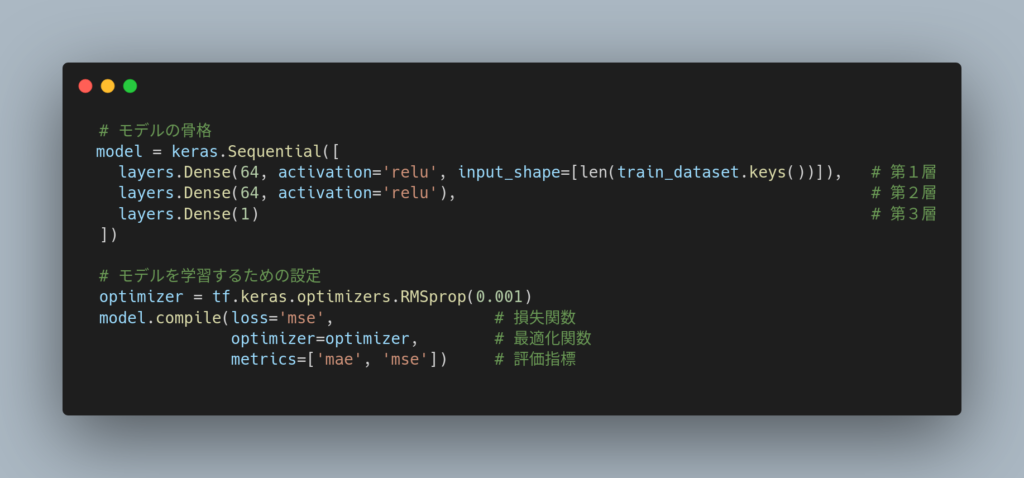
この10行にも満たない奇妙なプログラムが「モデル(model)」と呼ばれる ものです。
はたして、ピンときますでしょうか。
これまでのプログラミングに長年、慣れ親しんだ人にとって、違和感だらけのコードに見えるかもしれません。
まず、最初の5行のコードでモデルの骨格であるニューロンの層を3つの層をつくっています。
上から、
第1層は、入力層と呼ばれ、入力はデータセットの項目数( len(train_dataset.keys() ⇒9個)、出力が64個のニューロンを持つ層、
第2層は、中間層と呼ばれ、出力が64個のニューロンを持つ層、
第3層は、出力層と呼ばれ、出力が1個のニューロンを持つ 層
です。
構造を表示および図示すると、以下のような形状です。
_________________________________________________________________ Layer (type) Output Shape Param # ================================================================= dense (Dense) (None, 64) 640 _________________________________________________________________ dense_1 (Dense) (None, 64) 4160 _________________________________________________________________ dense_2 (Dense) (None, 1) 65 =================================================================
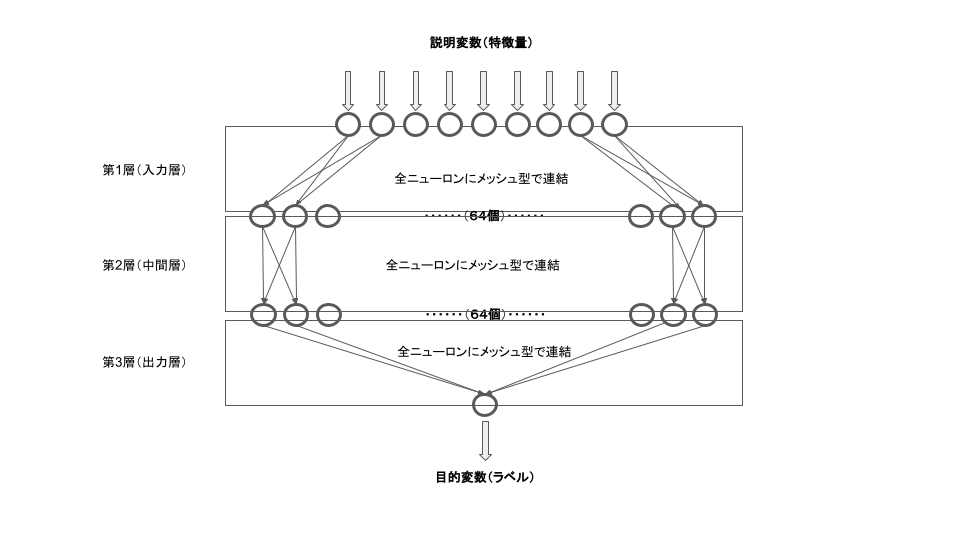
これは、すべて数値(整数、実数)の9個のパラメータを入力することで、最終的に数値の1個の出力結果を得ることができるモデルであることを示しています。(入力するパラメータは、説明変数(特徴量)と呼ばれ、出力結果は目的変数(ラベル)と呼ばれます)
第1層と第2層には、「activation=’relu’」という指定があります。
これは、各層からの出力を制御(制限)する活性化関数(activation)の名前です。’relu’とは、「ReLU関数」のことです。
このモデルでは、最終的にな出力を制御(制限)する必要がないため、第3層の出力層では、活性化関数の指定はありません。
後半の4行は、モデルを学習するための設定をするコードです。
この設定は、学習を効率的・効果的に行わせるためのもので、損失関数、最適化関数、そして、学習過程の状態を評価する評価指標を指定します。
損失関数(loss=’mse’)とは、学習過程で正解との差を計算する関数です。’mse’は、平均二乗誤差(MSE:Mean Squared Error)関数のことです。
最適化関数(optimizer = tf.keras.optimizers.RMSprop(0.001))は、学習過程において最適解を求めるために使われる関数です。 RMSprop がよく使われます。
評価指標(metrics=[‘mae’, ‘mse’])は、モデルの精度を示す数値です。学習過程において、指定した指標で誤差が減っていくことを観察することができます。誤差の指標として、’mae’(平均絶対誤差)と’mse’(最小二乗誤差)を指定しています。
学習過程と最終結果の評価指標を見れば、モデルの精度がどれくらいかを知ることができ、使い者になるモデルかどうかを判定することができます。
・モデルのパターン
モデルのパターンは、モデルの出力形態で見れば、入力したパラメータに従って結果を連続値(数字)で出力する「回帰」、入力したパラメータを区分けする「分類」の2種類だけです。
上記のモデルは、「回帰」であり、第3層の出力層に活性化関数は指定しません。
「分類」の場合、 2種類(True/Falseのような2つの分類)だけあれば、第3層の出力層に活性化関数は指定しませんが、3種類以上になれば、活性化関数(softmax)を指定し、各分類の確からしさ確率として出力させる制御をします。
一方、モデルのパターンである回帰、分類にかかわらず、入力層、中間層のプログラミングは同様なものです。
つまり、通常のプログラミングであれば、出力する結果毎に、ループ分、条件文、演算、関数コールを組み合わせて、データの計算処理=回帰、あるいは、データの判別処理=分類をしますが、 AIプログラミングでは、その必要はなく、 ただニューロンの層を重ねるだけです。基本的に、上記のモデルの作り方は変わりません。
変えるのは、学習データに応じて、層の数、出力ニューロンの数、活性化関数、損失関数/最適化関数/評価指標を変えるだけです。つまり、どんな入力、出力であっても、モデルのプログラミングは、同じようなコードとなります。
■ モデルの学習と評価
モデルだけでは、何の役にも立ちません。モデルは、学習させて、はじめて使えるようになります。
学習させることによって、ロジックの代わりとなるモデルの各層の出力ニューロンにデータ( ”重み”定数 )が蓄積され、使えるようになります。
ただし、これまでのようにソースコードを見てロジックを確認したり、理解することはできません。
学習には、学習用のデータが必要です。
学習用のデータは、入力データと出力データが1対1で関連付けられている必要があります。出力データは、入力データを処理したときの「結果」です。
(このような学習データは、あらかじめ入力データに対する出力データ(結果)がわかっているので、教師ありのモデルで使われる学習データです)
例えば、足し算のための学習データであれば、入力データが「1」と「1」の2つで、それらを足し算した結果である「2」を出力データとするようなデータのペアをたくさん用意します。
この場合、入力データと出力データの因果(原因と結果)が「足し算」という関係にあることが明白ですが、
通常、因果がわからないけれども、入力データと出力データだけは揃っているという状態から AIのモデルを始めることになります。
なぜならば、 AIプログラミング でモデルを創ること自体が「因果」関係を発見し、形作ることだからです。
現時点では、一般的なITエンジニアが作る AIのモデル は、教師ありのモデルです。
以下に、 TensolFlowのチュートリアル(回帰:燃費を予測する)より取得した学習データの例を載せます。
| MPG | Cylinders | Displacement | Horsepower | Weight | Acceleration | Model Year | USA | Europe | Japan |
| 18 | 8 | 307 | 130 | 3504 | 12 | 70 | 1 | 0 | 0 |
| 15 | 8 | 350 | 165 | 3693 | 11.5 | 70 | 1 | 0 | 0 |
| 18 | 8 | 318 | 150 | 3436 | 11 | 70 | 1 | 0 | 0 |
| 16 | 8 | 304 | 150 | 3433 | 12 | 70 | 1 | 0 | 0 |
| 17 | 8 | 302 | 140 | 3449 | 10.5 | 70 | 1 | 0 | 0 |
| 15 | 8 | 429 | 198 | 4341 | 10 | 70 | 1 | 0 | 0 |
| 14 | 8 | 454 | 220 | 4354 | 9 | 70 | 1 | 0 | 0 |
| 14 | 8 | 440 | 215 | 4312 | 8.5 | 70 | 1 | 0 | 0 |
| 14 | 8 | 455 | 225 | 4425 | 10 | 70 | 1 | 0 | 0 |
| 15 | 8 | 390 | 190 | 3850 | 8.5 | 70 | 1 | 0 | 0 |
| … | … | … | … | … | … | … | … | … | … |
この学習データは、リッター当たりの燃費(KM)であるMPGを出力データ(目的変数)とし、他のデータを入力データ(説明変数)としたものです。
ここで、すべて数値であることを認識する必要があります。モデルの入力と出力は数値でなければなりません。文字列をモデルで扱うことはできないからです。
学習の前に、出力データと入力データを分離します。
そして、以下のように、説明変数である入力データを標準化((値-平均値)/標準偏差)し、値の範囲を縮小化します。一般的に値の取る範囲を狭めることで、学習時間の削減や精度確保がし易くなります。
| Cylinders | Displacement | Horsepower | Weight | Acceleration | Model Year | USA | Europe | Japan |
| -0.86935 | -1.00946 | -0.78405 | -1.0253 | -0.37976 | -0.5164 | 0.774676 | -0.46515 | -0.49523 |
| -0.86935 | -0.53022 | -0.44281 | -0.1188 | 0.624102 | 0.84391 | 0.774676 | -0.46515 | -0.49523 |
| 1.483887 | 1.482595 | 1.44714 | 1.736877 | -0.73828 | -1.06052 | 0.774676 | -0.46515 | -0.49523 |
| -0.86935 | -0.86569 | -1.09904 | -1.0253 | -0.30805 | 1.660094 | 0.774676 | -0.46515 | -0.49523 |
| -0.86935 | -0.94237 | -0.99405 | -1.0016 | 0.875068 | 1.115971 | -1.28675 | -0.46515 | 2.012852 |
| 0.30727 | 0.351586 | -0.39031 | 0.260397 | 0.58825 | 0.571849 | 0.774676 | -0.46515 | -0.49523 |
| -0.86935 | -1.01904 | -1.17779 | -1.21134 | 1.161885 | 1.115971 | -1.28675 | -0.46515 | 2.012852 |
| -0.86935 | -0.47271 | -0.99405 | 0.307796 | 2.237451 | 1.115971 | -1.28675 | 2.143005 | -0.49523 |
| 0.30727 | 0.025702 | -0.25907 | 0.132419 | 0.337285 | -0.5164 | 0.774676 | -0.46515 | -0.49523 |
| … | … | … | … | … | … | … | … | … |
入力データの項目毎の標準化のための平均値 、標準偏差は、学習データ全体で集計した統計データを使います。
これら 平均値と、標準偏差は、モデルを使うときにも、標準化した入力データを設定します。
したがって、標準化に使った平均値 、標準偏差は、保存しておき、モデルを使う時にも利用できるようにしておく必要があります。
学習データを使ってモデルを学習させるには、 次のfit関数に、入力データ(train_dataset)と出力データ(train_labels)を指定し、実行するだけです。EPOCHSは、学習データを使って繰り返す回数(300回)です。
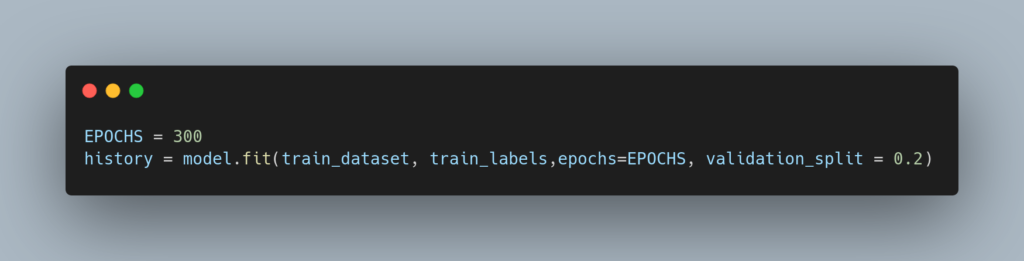
validation_split = 0.2と指定してますが、これは入力データと出力データから 評価指標を生成するための評価データ を抽出する割合(20%)を指定することを意味しています。
学習データは、実際にモデルを学習させるために使う訓練データと、評価指標を生成するための評価データに分けます。
評価データは、学習には使われません。自動的に、逐次、訓練データによって学習されたモデルに評価データが入力され、その出力結果と、テストデータの出力データを比較し、誤差を計算するために使われます。
学習中、学習の過程が、以下のように表示されます。また、その様子を図にしたものを載せます。
Epoch 1/300 8/8 [==============================] - 10s 658ms/step - loss: 599.9429 - mae: 23.1547 - mse: 599.9429 - val_loss: 556.3746 - val_mae: 22.2135 - val_mse: 556.3746 Epoch 2/300 8/8 [==============================] - 0s 39ms/step - loss: 505.1933 - mae: 21.0954 - mse: 505.1933 - val_loss: 496.6354 - val_mae: 20.8324 - val_mse: 496.6354 Epoch 3/300 8/8 [==============================] - 0s 42ms/step - loss: 463.9693 - mae: 20.2715 - mse: 463.9693 - val_loss: 437.3376 - val_mae: 19.3800 - val_mse: 437.3376 Epoch 4/300 8/8 [==============================] - 0s 33ms/step - loss: 407.0854 - mae: 18.5471 - mse: 407.0854 - val_loss: 375.9893 - val_mae: 17.7812 - val_mse: 375.9893 Epoch 5/300 8/8 [==============================] - 0s 34ms/step - loss: 369.1436 - mae: 17.7153 - mse: 369.1436 - val_loss: 313.9082 - val_mae: 16.0161 - val_mse: 313.9082 … Epoch 295/300 8/8 [==============================] - 0s 43ms/step - loss: 5.3634 - mae: 1.5502 - mse: 5.3634 - val_loss: 8.3566 - val_mae: 2.2006 - val_mse: 8.3566 Epoch 296/300 8/8 [==============================] - 0s 23ms/step - loss: 5.2324 - mae: 1.4909 - mse: 5.2324 - val_loss: 8.3972 - val_mae: 2.1801 - val_mse: 8.3972 Epoch 297/300 8.2688 Epoch 298/300 8/8 [==============================] - 0s 14ms/step - loss: 3.9119 - mae: 1.3440 - mse: 3.9119 - val_loss: 8.2392 - val_mae: 2.1521 - val_mse: 8.2392 Epoch 299/300 8/8 [==============================] - 0s 16ms/step - loss: 4.4657 - mae: 1.4899 - mse: 4.4657 - val_loss: 8.4008 - val_mae: 2.1206 - val_mse: 8.4008 Epoch 300/300 8/8 [==============================] - 0s 20ms/step - loss: 4.4969 - mae: 1.4852 - mse: 4.4969 - val_loss: 8.3084 - val_mae: 2.1949 - val_mse: 8.3084
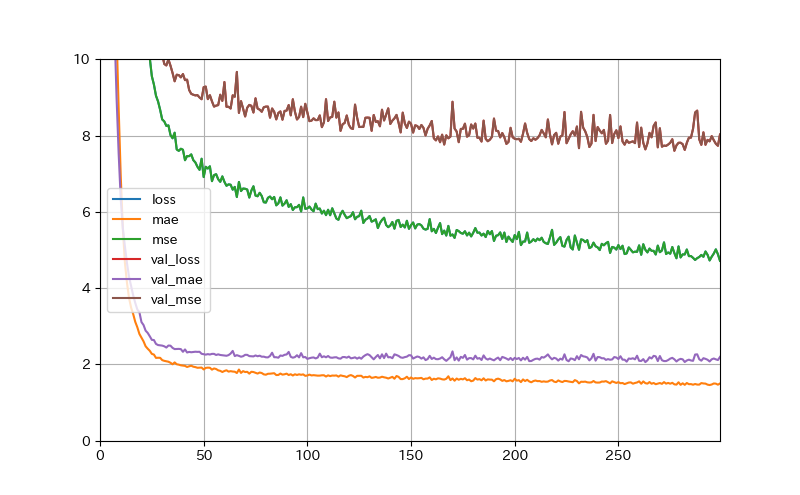
見るべき指標は、 maeとmseではなく、val_maeとval_mseの方です。
これらが収束し、そして両者の差がない(訓練の結果が正しい)ことが必要です。
これらはモデルの作成時に指定した評価指標(maeとmse)ですが、 maeとmse は訓練データによる値であり、 val_maeとval_mse は評価データを使って検算した値です。したがって、 val_maeとval_mse が、学習されたモデルがどれだけ実用的であるかを示しています。
これらの値が大きければ、誤差が大きすぎて、そのモデルは使い物にはなりません。
たとえば、実際使ってみたら、1+1の結果を3とした間違った値を出力してしまいます。
そうなったとき、モデルの層の数、出力ニューロンの数、活性化関数、損失関数/最適化関数/評価指標などを変えてチューニングする必要があります。(訓練データへの過学習の抑制のためドロップアウト層を追加する必要もあります)
また、学習データに不備がある場合も十分にあります。その場合、入力データの項目を増減させたり、不足しているデータを追加するために学習データの収集をやり直す必要も出てきます。
さらに、そもそも、モデル化することができない、つまり、事前に考えた仮説が間違っていて因果関係のないモデルを創ろうとしているのではないかと疑いを持って、再度、ふりだしに戻って仮説の検討から始めなければならないこともあるでしょう。いわゆる「無理ゲー」というやつです。
■ 学習後のモデルを使うためのプログラミング
学習後の モデルを使うには、学習データとは別の入力データを指定し、Predict関数を呼び出します。その結果、出力データが返却されます。これを予測データと言います。
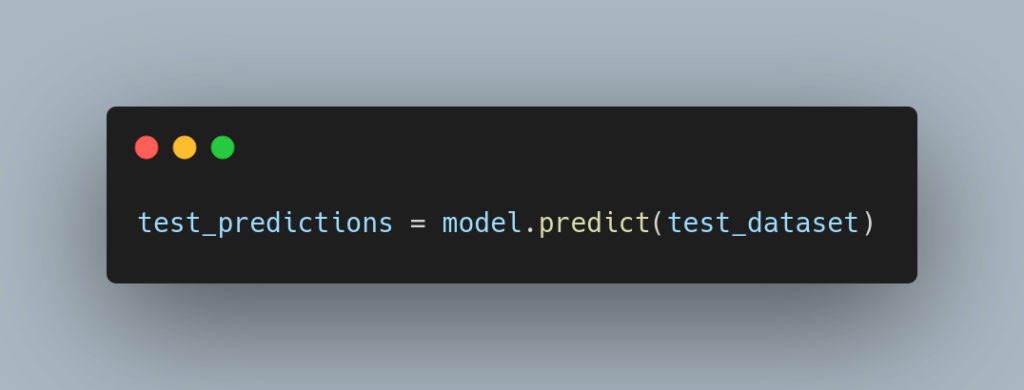
予測データは、以下のように返却されます。
[[15.847161 ] [10.755352 ] [ 9.9577265] … [36.00261 ] [38.402367 ] [29.130249 ]]
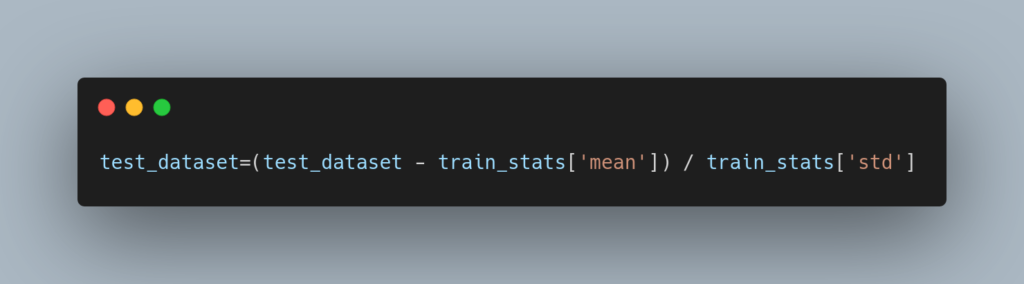
忘れてはいけないのは、このモデルは標準化された入力データを使って学習されている点です。
予測で使う入力データも以下のように、事前に標準化する必要があります。
■ 学習データの仕様
前述したように学習データは数値でなければなりません。さらに、数値にするにしても幾つかの仕様があります。
・入力データ(説明変数)の数値が連続値であること
例えば、価格は、連続値で、100円、101円・・・といったように連続して変化します。
しかし、種別を意味するようなデータ(USA=0、Europe=1、Japan=2)などは、そうではありません。連続値ではなく、個々の分類を示しています。
この場合、OnHotベクトルと呼ばれるものに置き換えて、入力データとする必要があります。
OnHotベクトルとは、値のパターンを表のように横展開し、有り(1)無し(0)だけのデータに変換することです。こうすれば、連続値として変化するように見せることができます。
例えば、本当は、 USA=0、Europe=1、Japan=2 のデータを、以下のように該当の種別を示すデータに1を立てるようなデータに変換します。
| パターン | USA | Europe | Japan |
| USA=0の場合 | 1 | 0 | 0 |
| Europe=1の場合 | 0 | 1 | 0 |
| Japan=2の場合 | 0 | 0 | 1 |
・出力データ(目的変数)の数値は、連続値である必要はない
モデルのパターンが、回帰ではなく、分類を目的としたモデルの場合、出力データ(目的変数)は、
入力データと違って、たとえ種別を示すデータであっても数値でさえあれば、OneHotベクトル化する必要はありません。
したがって、たとえば、 上記を出力データ(目的変数)とするので、USA=0、Europe=1、Japan=2 のままの数値で構いません。
ただし、予測の際、モデルから出力されるデータは、OneHotベクトル化されて出力されます。
前述したように、通常、出力層の活性化関数に「sigmoid」を設定するためです。
その値は、0、1ではなく、以下のように各々のパターンの確率を示す数値が設定され、その中から、一番高い確率のパターンを結果として選択することになります。
| USA | Europe | Japan |
| 0.9 | 0.05 | 0.05 |
| 0.1 | 0.85 | 0.05 |
| 0.93 | 0.03 | 0.95 |
・ 入力データ(説明変数) と 出力データ(目的変数) の配列の次元数
モデルへの入力と出力は、配列で指定するため、学習データも次のような配列として準備する必要があります。
1次元 → [ 1,2,3,4,5,6,7,8,9… ]
2次元 → [ [ 1,2,3 ],[ 4,5,6 ],[ 7,8,9 ] , … ]
3次元 → [ [ [ 1,2,3 ],[ 4,5,6 ],[ 7,8,9 ],…] , [ [ 1,2,3 ],[ 4,5,6 ],[ 7,8,9 ],…] , …]
ただし、入力データの配列の次元数は、「2次元以上」である必要があります。
また、出力データの配列の次元数は、「2次元」である必要があります。
学習データの配列は、PandasまたはNumpyの配列を使いますが、
Pandasは、1次元と2次元の配列しか作成できないので、3次元以上の配列を作成する場合、Numpyを使う必要があります。
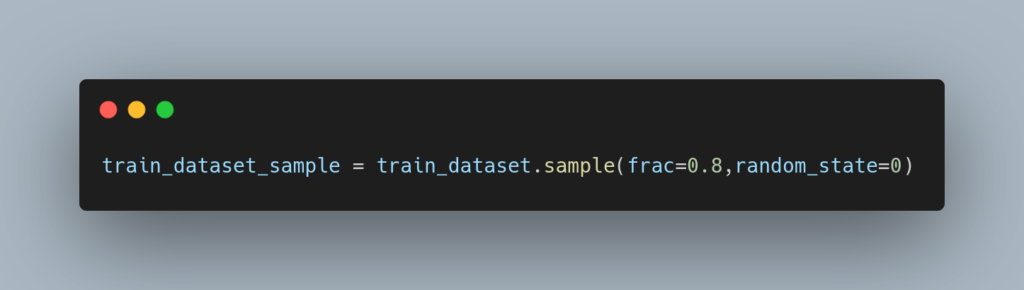
・入力データの順番も学習精度を左右する
学習データをモデルに入力する順番も学習精度に影響します。降順・昇順の整列されているよりも、以下のようにしてランダムに配置する方が効果があります。
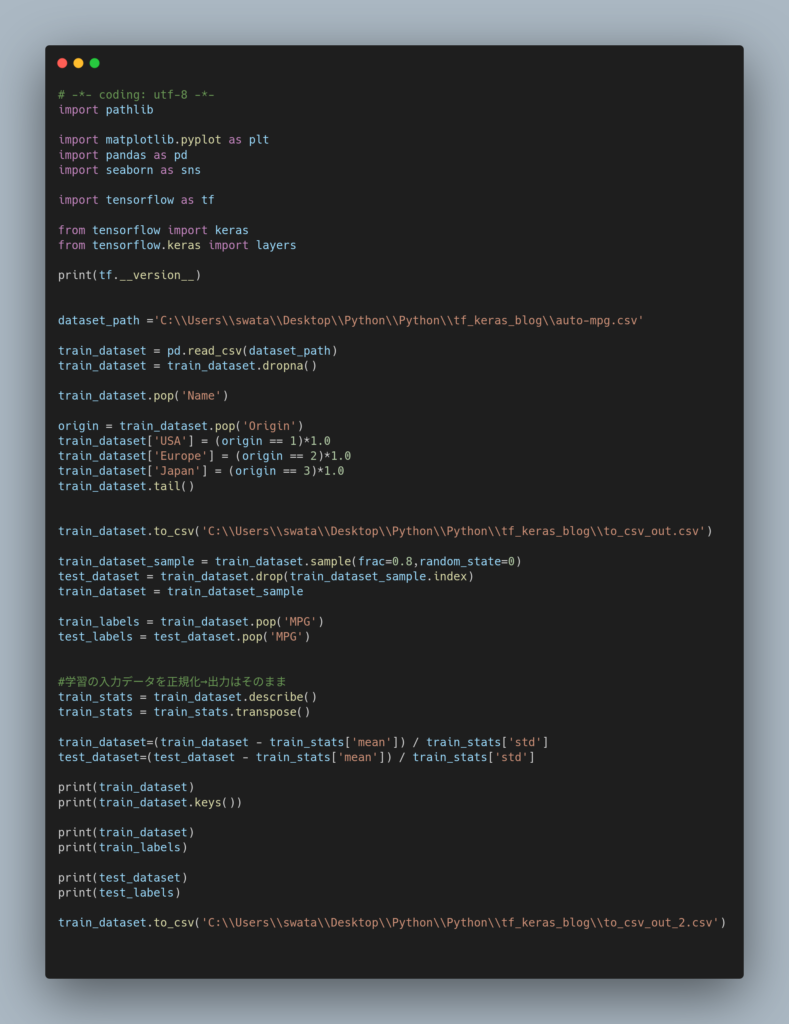
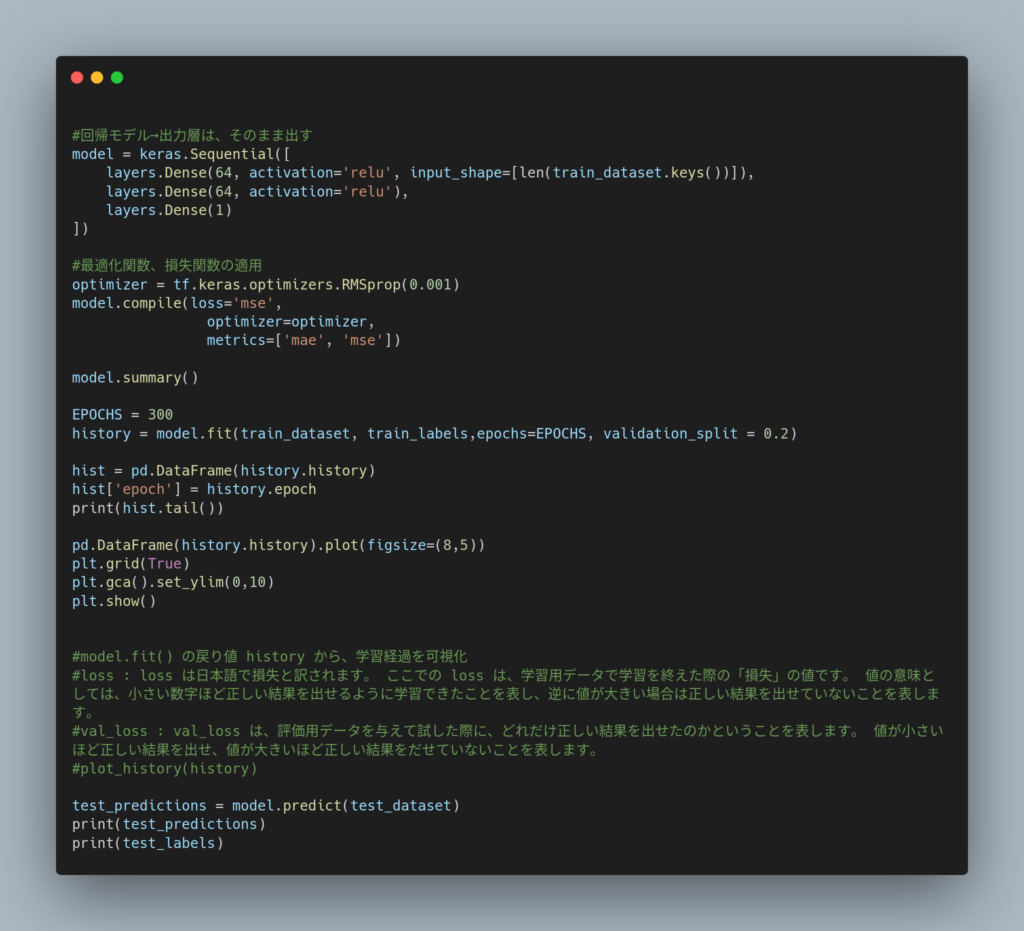
■ サンプルコード全文
上記のサンプルコード全文を以下に示します。
(TensolFlowのチュートリアル(回帰:燃費を予測する) を改変したものです。学習データは、元のリンクから取得してください)
■ まとめ
想像するよりずっと大変なのが、学習データを準備することです。
学習データの元データは、以下から収集することになります。
1)WebサイトやSNSからスクレイピング
2)RDB
3)ファイル
まず、上記の生データがどのサーバ、誰が持っているのかを調査し、サンプルのデータを入手しなければなりません。もし紙のデータしかない場合、それらからデータを登録・生成する作業も必要です。
このような作業は、これまでもデータベース構築において、実施されてきたことです。
巷では、インターネットを始めビックデータがそこら中にあるように言われていますが、実際に AIを創ろうとすると、そう簡単には欲しい特徴量を持った一定量のデータを入手できないことに気がつきます。
一方、同じようなデータだけをたくさん集めても意味がありません。
例えば、マンション価格を知るために、不動産業者サイトからの販売物件をスクレイピングをしても、入手できるデータは量もパターンも少なく、また、実際に顧客にいくらで売れたかを知ることはできません。それは不動産業者の内部情報として蓄積されており、外部からはアクセスすることはできません。
そうなると、 AI を創る前に、頓挫してしまいます。そのため、 AIプログラミングについて語るより前に、どうやってデータを入手するかを明確にすることが先決でしょう。
そのためには、時にはデータを外部から購入したり、社内の各部署との協力を得て収集するなど、金銭面、組織面での対応が必要になるでしょう。
また、 AIプログラミングは、 ブラックボックスプログラミングであり、モデルのロジックを最初に決めることができません。従来までの設計によってロジックを決めるホワイトボックスプログラミングとは全く異なります。
したがって、ウォータフォール型の開発では対応できず、アジャイル開発などのインクリメンタル型でないと不可能です。そのため、どれだけの工数が必要になるのかを見積もることも難しくなります。
うまくいけば使えるモデルを作りだすことができますが、できたモデルも、多大な工数を費やしたにも関わらず適用範囲が極端に狭い結果となる可能性も大きいと考えられます。
したがって、AIプログラミングは 、エンジニアリングではなく、サイエンスの側面が大きく、製造ではなく、発見を目的とするものであることを理解しておく必要があります。
現状、業務システムにおいて、データ分析は、RDBによる検索・集計機能によって実現されています。
たとえば、過去の売上データを月別に商品単位で集計すれば、翌年の月別・商品別の需要予測は簡単にできます。
あえて、このような既存で予測可能な処理を、 AIプログラミング によるモデルで置き換えることに意味はありません。それ以外で、現状カバーできない対象について、予測モデルを創るために AIプログラミング は適用されるべきです。
ただし、その AIプログラミングの適用範囲を探ることは、緻密で深い現状分析に基づき課題を発見しなければなりません。これも泥臭く、骨の折れる作業です。
AIプログラミング を既存技術の上に組み込む取り組みは、現状を超えるという意味で価値のあることです。しかし、AIプログラミング によって既存技術を刷新できるようなレベルとなるまでは、まだ時間が必要でしょう。
ソフトウェア開発・システム開発業務/セキュリティ関連業務/ネットワーク関連業務/最新技術に関する業務など、「学習力×発想力×達成力×熱意」で技術開発の実現をサポート。お気軽にお問合せ下さい






